一、引言

出发点：

  • 在对缝的间隙和阶差的测量过程，对缝结构的正确，完整提取是非常重要的。
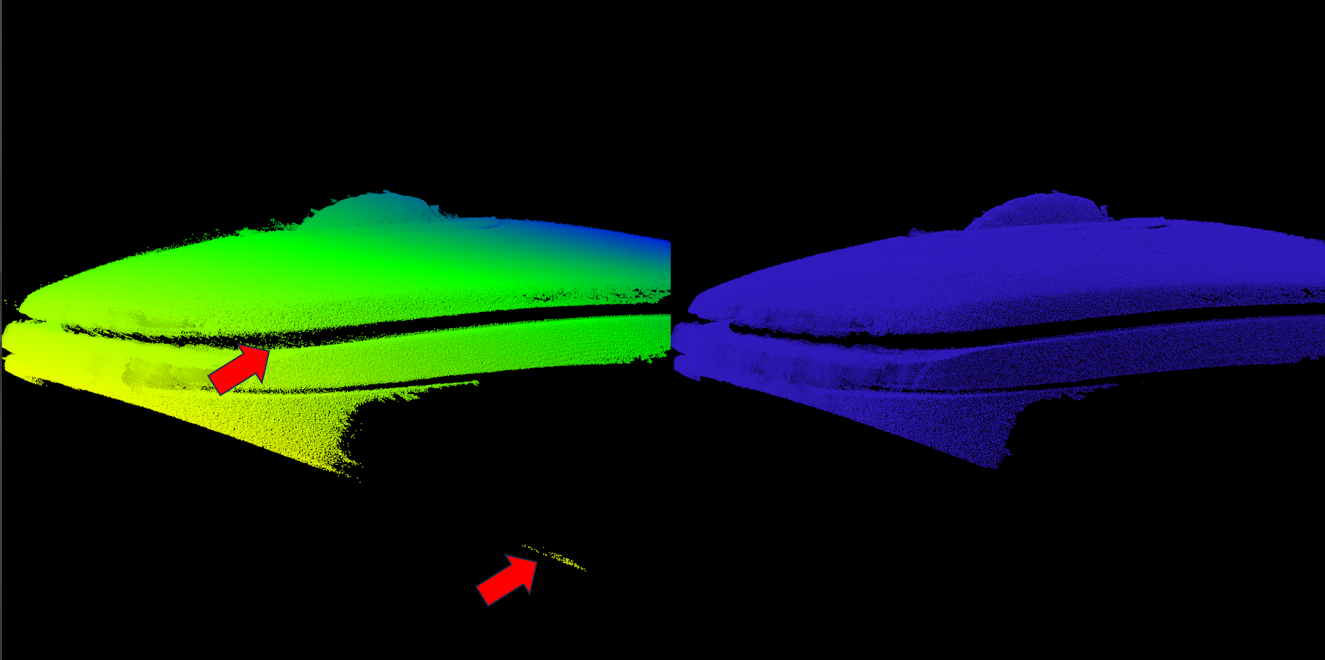
  • 实际的点云采集过程中，易受到环境光照条件，以及被测量物体的表面反光条件的影响，点云的密度分布是不规律的，会收到光环境的影响，不再是传统意义上的在边界部分，或者拐角部分的密度大，密度差异不一致 —— 对缝结构采取 密度差异提取不可行。
  • 融合曲率与边界特征提取，能极大的提高特征提取算法的鲁棒性。

如下图：点云的密度分布不均匀，采用密度分割 无法将特征提取。

密度分布不均匀

因此提出曲率边界融合特征提取：

  • 点云的曲率特征能够很大程度上的保留关键特征信息
  • 点云的边界特征能够保留轮廓的信息

二、实现

曲率估计

PCL中的曲率有两个 一个是 NormalEstimation中的曲率 ，另一个是PrincipalCurvaturesEstimation .

  • 前者表示是表面曲率，即表示表面的起伏程度；
  • 后者见下图，曲率估计出来有两个值，一个最大，一个最小曲率—>即可求平均曲率
image-20240316171027015 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
   // 计算
pcl::PrincipalCurvaturesEstimation<pcl::PointXYZ, pcl::Normal, pcl::PrincipalCurvatures>pointCur;
pcl::PointCloud<pcl::PrincipalCurvatures>::Ptr cloudCurvature(new pcl::PointCloud<pcl::PrincipalCurvatures>);
pointCur.setInputCloud(cloud);
pointCur.setInputNormals(normals);
pointCur.setSearchMethod(tree);
pointCur.setRadiusSearch(0.5);
pointCur.compute(*cloudCurvature);
// 保存
int cloudCurSize = cloudCurvature->size();
vector<float> tempCur;
float meanCur = 0.0, curThreshold = 0.001;
   std::unordered_set<int> pointIdxSet;
       
for (size_t i = 0; i < cloudCurSize; i++){
	meanCur = (cloudCurvature->points[i].pc1 + cloudCurvature->points[i].pc2) / 2; // 平均曲率
	tempCur.push_back(meanCur);
	if (meanCur > curThreshold){
                pointIdxSet.insert(i);
	}
   }

边界计算

参考文献：Bendels G H , Schnabel R , Klein R .Detecting Holes in Point Set Surfaces[J].Journal of WSCG, 2006, 14.

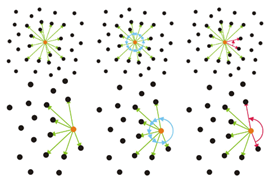
边界计算采用BoundaryEstimation，其原理即：

  • 搜索每个点的邻域信息，建立点 到其邻域点的连线
  • 统计每两个连线之间的夹角值，
  • 超过给定的阈值即为边界点
image-20240316172453892

三、结果

曲面的对缝：

image-20240316172630043

平面的对缝：

image-20240316172708011

均能提取出对缝特征，并且在划分测量小区间方面，融合特征算法也表现不错。划分的区间数量稳定。

区间划分示意图：

image-20240317165722491

平面：

平面
融合 （个） 仅曲率 仅边界
1 57 57 59
0.9 57 57 57
0.8 58 58 58
0.7 57 57 57
0.6 55 55 56
0.5 55 55 60
0.4 57 57 59
0.3 55 55 57
0.2 57 57 44
0.1 57 57 47
0.075 57 57 57
0.050 56 56 56
0.025 56 10 56
0.000 61 0 61

曲面：

斜面
融合 曲率 边界
1 77 77 73
0.9 77 77 70
0.8 78 78 73
0.7 78 78 72
0.6 76 76 71
0.5 76 76 73
0.4 76 76 47
0.3 76 76 47
0.2 72 72 30
0.1 74 74 47
0.075 69 70 28
0.050 76 19 72
0.025 76 6 76
0.000 76 0 76